
2個の電荷 Q1[C]、Q2[C] の間には、Q1 と Q2 を結ぶ直線方向に静電力 F[N] が働く。誘電率を ε[F/m]、Q1、Q2 の間の距離を r[m] とすると、静電力 F は次式で表せる。
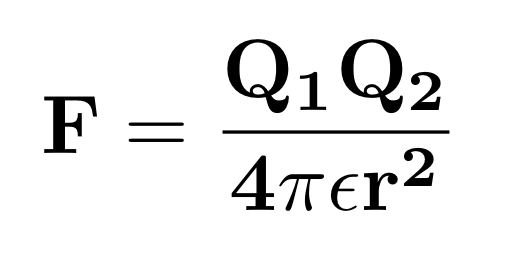
つまり、静電力 F は、電荷 Q1、Q2 の積に比例し、Q1、Q2 の距離の2乗に反比例する。また、電荷 Q1、Q2 が 両方とも同符号(ともにプラス、またはマイナス)の場合は、反発する方向に静電力が働き、電荷 Q1、Q2 が異符号(プラスとマイナス)の場合は、引き合う方向に静電力が働く。

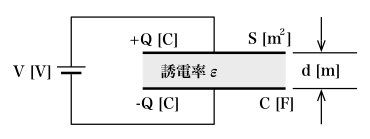
コンデンサに蓄えられる電荷量を Q クーロン [C]、コンデンサの両極板間の電位差を V ボルト [V]、静電容量を C ファラド [F] とすると、次式が成り立つ。
Q = CV
また、平行平板の面積を S[m2]、間隔を d[m]、平板間の誘電体の誘電率を ε とすると、平行平板の静電容量 C[F] は、次式で表すことができる。

つまり、静電容量を大きくするためには、次の3つの方法がある。
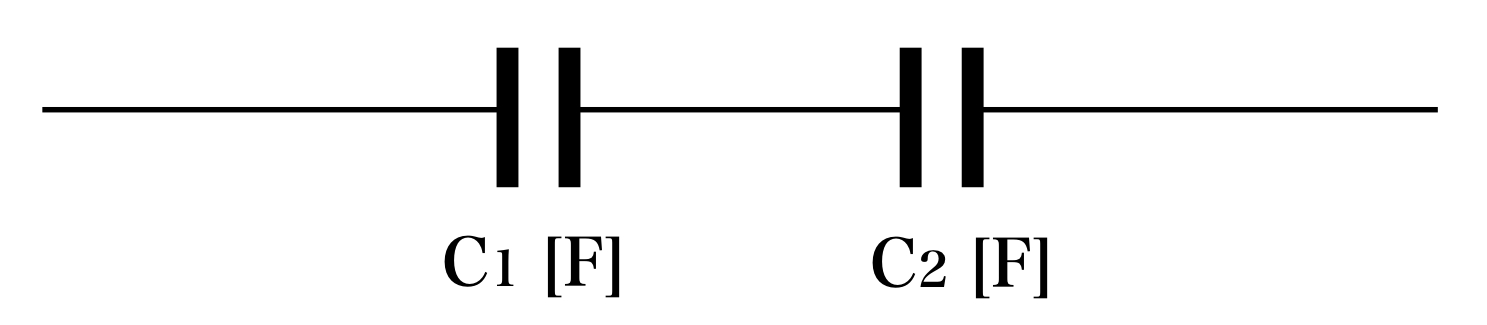
静電容量 C1[F]、C2[F] の2つのコンデンサを直列に接続した場合の合成静電容量 C は次式で表される。


静電容量 C1[F]、C2[F] の2つのコンデンサを並列に接続した場合の合成静電容量 C は次式で表される。
C = C1 + C2
次の文章の[ ]内に、解答群の中から、最も適したものを選び、その番号を記せ。
静電容量が 3C ファラドのコンデンサに V ボルトの直流電圧を加えると、コンデンサに蓄えられる電荷の量 Q は、[ ] クーロンで表される。

電荷量 Q は,以下の式で求められる。
Q = CV
このとき C が「3C」であるので,それを代入すると,
Q = 3CV
となり,答えは 3CV となります。
次の文章の[ ]内に、解答群の中から、最も適したものを選び、その番号を記せ。
2 個の電荷 Q1、Q2 の間には、Q1 と Q2 を結ぶ直線方向に力が働く。その大きさは、Q1 と Q2 のそれぞれの電荷の量の積に比例し、Q1 と Q2 間の距離の[ ] 乗に反比例する。(1) 1/2 (2) 1 (3) 2
クーロンの法則より,
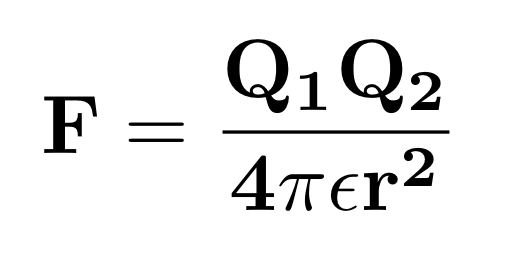
静電力 F は,2つの電荷量の積に比例し,2つの電荷量間の距離の2乗に反比例する。
次の文章の[ ]内に、解答群の中から、最も適したものを選び、その番号を記せ。
平行電極板で構成されているコンデンサの静電容量を大きくする方法の一つに、[ ] 方法がある。
(1) 電極板の面積を小さくする (2) 電極板の間隔を大きくする (3) 電極板間に誘電率の値が大きい物質を挿入する
平行平板の静電容量 C[F] は、次式で表すことができるから,

静電容量を大きくするためには,
の3つの方法がある。
次の文章の[ ]内に、解答群の中から、最も適したものを選び、その番号を記せ。
静電容量の単位であるファラドと同一の単位は、[ ] である。
(1) ボルト/アンペア (2) ジュール/クーロン (3) クーロン/ボルト
電荷量 Q は,以下の式で求められる。
Q[C] = C[F]・V[V]
これを静電容量 C を求める式に変形すると,
C[F] = Q[C] / V[V]
右辺の式の単位は,[C/V]となる。つまり答えはクーロン/ボルトとなる。