ネットワーク接続技術者工事担任者試験 DD 第3種(第I部 電気通信技術の基礎)の「電気回路」について説明しています。
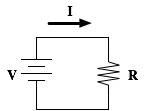
電気回路に流れる電流は、回路に加えた電圧に比例し、抵抗に反比例する。電流をI アンペア[A]、電圧をV ボルト[V]、抵抗をR オーム[Ω]とすると、それらの関係は、次式で表される。
![]()

各端子間の電圧を V、V1、V2、V3、電流を I、I1、I2、I3、抵抗を R1、R2、R3 とする。 このとき、端子 a-b 間の合成抵抗は、各抵抗の総和で表され、合成抵抗を R とすると、次式で表現される。
合成抵抗 R = R1 + R2 + R3
また、直列回路の場合、各抵抗を流れる電流はすべて等しくなる。
I = I1 = I2 = I3
そのため、各電圧と抵抗には以下の関係が成り立つ。
V = V1 + V2 + V3 , V1 : V2 : V3 = R1 : R2 : R3 (分圧)

各抵抗を R1、R2、R3、端子 a-b 間の電圧を V 、各抵抗の電圧を V1、V2、V3、端子 a-b 間の電流を I、各抵抗を流れる電流を I1、I2、I3 とする。
このとき、端子 a-b 間の合成抵抗は、各抵抗の逆数の和の逆数となる。合成抵抗を R とすると、次式で表現される。

また、並列回路の場合、端子 a-b 間の電圧と各抵抗の電圧はすべて等しくなる。
![]()
そのため、各電流と抵抗には以下の関係が成り立つ。


電圧計は測定する2点間に並列に接続する。
電圧計の測定範囲を拡大するためには、電圧計に対して直列に抵抗 Rm(これを倍率器という)を接続する。電圧計の内部抵抗を r、測定する電圧を V 、電圧計の最大測定電圧を V0 とすると、拡大される電圧の倍率 m は次式で表される。

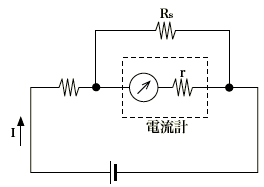
電流計は測定したいところに直列に接続する。
電流計の測定範囲を拡大するためには、電流計に対して並列に抵抗Rs(これを分流器という)を接続する。電流計の内部抵抗をr、測定する電流をI、電流計の最大測定電流をI0 とすると、拡大される電流の倍率n は次式で表される。
![]()
電気抵抗は、導体の長さl[m] に比例し、断面積A[m2] に反比例する。
電気抵抗率(単に抵抗率ともいう)をρ[Ω・m]、長さをl[m]、断面積をA[m2] とすると、抵抗R[Ω] は、次式で表される。
![]()
この節では,いくつかの練習問題を解いてみよう。解答では,うまい解法よりは,なるべく初歩的知識だけで解ける方法を説明したつもりです。
次の各文章の[ ]内に、それぞれの解答群の中から、最も適したものを選び、その番号を記せ。
図-1に示す回路において、抵抗 R2 に 6 アンペアの電流が流れたとき、この回路に接続されている電池 E は、[ ]ボルトである。ただし、電池の内部抵抗は無視するものとする。
(1) 48 (2) 53 (3) 56 (4) 63 (5) 66
並列部分の抵抗 R2,R3にかかる電圧は等しく,電圧を V2とすると,
V2 = 6 [A] × 3 [Ω] = 18 [V]
となります。つぎに抵抗 R3 を流れる電流 I3 は,
I3 = V2[V] / 2 [Ω] = 18 / 2 = 9 [A]
となります。また,抵抗 R1 を流れる電流 I1 は,並列部分で分流されているので,
I1 = 6 [A] + I3 [A] = 6 + 9 = 15 [A]
となります。このとき電圧 E は,分圧されている電圧の合計になりますから,
E = V1 + V2
と表されるので,後は,電圧 V1 を求めれば,解答にたどり着けます。
V1 = I1 [A] × R1 [Ω] = 15 × 3 = 45 [V]
∴ E = V1 + V2 = 45 + 18 = 63 [V]
最大目盛がいずれも 20 アンペアである直流電流計 A1 及び A2 がある。これらの直流電流計の針が最大目盛に振れたときの端子電圧降下は、A1 では 40 ミリボルト、A2 では 60 ミリボルトである。この二つの電流計 A1 及び A2 を図 1 に示すように接続し、端子 a - b 間に 15 アンペアの電流を流すと、直流電流計 A2 の値は、[ ] アンペアである。
(1) 2 (2) 4 (3) 6
まず,電流計 A1,A2 の内部抵抗を求めます。
A1の内部抵抗 = 40 [mV] / 20 [A] = (40 × 10-3) / 20 = 2 × 10-3 [Ω]
A2の内部抵抗 = 60 [mV] / 20 [A] = (60 × 10-3) / 20 = 3 × 10-3 [Ω]
となります。つぎに回路全体の合成抵抗を求めます。
1/合成抵抗
= {1/(2 × 10-3)} + {1/(3 × 10-3)}
= (1/2 + 1/3) × 103 = (3 + 2) / (2 × 3) × 103
= 5 / 6 × 103
∴ 合成抵抗 = 1 / (5 / 6 × 103) = 6 / 5 × 10-3 [Ω]
となります。このとき回路に 15 [A] の電流が流れるので,そのときの電圧は,
電圧 = 15 [A] × 6 / 5 × 10-3 [Ω] = 18 × 10-3 [V]
となります。このとき電流計 A2 にも同じ電圧がかかるので,そのときの電流は,
A2の電流 = (18 × 10-3) [V] / (3 × 10-3) [Ω] = 6 [A]
となります。
原始的な解法は上のとおりですが,実際には,「分流の法則」を使えば,各電流計の内部抵抗を求めた後,簡単な計算で答えを求めることができます。
A2の電流 = {A1の内部抵抗 / (A1 の内部抵抗 + A2 の内部抵抗)} × 回路電流 [A]
A2の電流
= {2 × 10-3 [Ω] / (2 × 10-3 [Ω] + 3 × 10-3 [Ω])} × 15 [A]
= {2 × 10-3 [Ω] / 5 × 10-3 [Ω]} × 15 [A]
= 6 [A]
図 1 に示す回路において、端子 a - b 間の合成抵抗は、[ ] オームである。
(1) 7 (2) 8 (3) 9
図 1 の回路の等価回路は,図のとおりになります。後は,順番に合成抵抗を計算すればいいので,まずは,5 [Ω] と 20 [Ω] の並列部分の合成抵抗1を計算します。
1/合成抵抗1 = 1 / 5 + 1 / 20 = (4 + 1) / 20 = 5 / 20 = 1 / 4
∴ 合成抵抗1 = 4 [Ω]
つぎに求めた合成抵抗1と 8 [Ω] の直列回路部分の合成抵抗2を計算します。
合成抵抗2 = 合成抵抗1 + 8 [Ω] = 4 + 8 = 12 [Ω]
つぎに求めた直列部分の合成抵抗2と 4 [Ω] の並列部分の合成抵抗3を計算します。
1/合成抵抗3 = 1 / 合成抵抗2 + 1 / 4 [Ω]
= 1 / 12 + 1 / 4
= (1 + 3)/ 12 = 4 / 12 = 1 / 3
∴ 合成抵抗3 = 3 [Ω]
最後に求めた合成抵抗3と 6 [Ω] の直列部分の合成抵抗を求めます。ここで求められた合成抵抗が答えとなります。
合成抵抗 = 合成抵抗3 + 6 [Ω] = 3 + 6 = 9 [Ω]
断面が円形の導線の抵抗値は、導線の長さを 9 倍にしたとき、直径を [ ] 倍にすれば、変化しない。
(1) 1/3 (2) 3 (3) 9
いま導線の抵抗を R,抵抗率を ρ,長さを l,断面積を A としたとき,つぎの関係が成り立ちます。
R = ρ × (l / A) [Ω]
このとき断面が円形の導線の断面積 A は,半径を r とすると,
A = 半径 × 半径 × 円周率 = πr2
となります。いま直径を d とすると,r = d / 2 ですから,
A = πr2 = π(d / 2)2 = πd2 / 4
となります。これを抵抗の式に代入すると,
R = ρ × (l / A) = ρ × {l / (πd2 / 4)} = ρ × (4l / πd2)
となります。このとき長さ l を 9 倍にして,直径を x 倍にすれば変化しないので,
R = ρ × (4l / πd2) = ρ × {4(l × 9) / π(xd)2}
となりますから,求める x は,つぎのようになります。
ρ × (4l / πd2) = ρ × {4(l × 9) / π(xd)2}
ρ × (4l / πd2) = ρ × (36l / πx2d2)
4 = (36 / x2)
4x2 = 36
x2 = 9
x = 3